Evolution of Cooperation

Computer Science and Music major Kenan Bitikofer worked with David Housman on a Maple Scholars project modeling the evolution of cooperation in a society.  Kenan created and analyzed simulations of populations where players (could be people, nations, or bacteria) may choose to cooperate with or exploit their neighboring players.  Once the neighboring players have made their decisions, it is always beneficial to a player to choose to exploit; however, mutual cooperation is better than mutual exploitation.  Under what circumstances with a society playing such a game evolve to cooperate?

Maple Scholars is an eight-week summer program that gives students the opportunity to participate in independent research projects alongside Goshen College faculty of various disciplines.   Scholars keep each other informed of their progress in weekly seminars, and the program ends with a celebration involving a public poster session, presentations, and a dinner.

Kenan’s final report can be accessed from David Housman’s Undergraduate Research Page.  Here is his abstract and one of the diagrams summarizing his results.

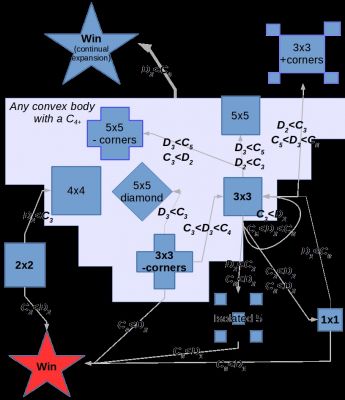
Much research has been devoted to specific two person, symmetric, binary decision (STPBD) games in the spatial context of cellular neighborhoods. Nowak first proposed a spatial model for these games, in which players are located in a square lattice and play a Prisoner’s Dilemma (PD) game against each of their neighbors, using either the strategy of AllD or AllC. To move the simulation into the next generation, each cell will compare its cumulative score to that of its neighbors, and adopt the most successful strategy it finds. Nowak categorized those PD games with payoffs S = P = 0, R = 1, and T = b(b > 1). His research revealed different end behaviors for values of the variable b, which are mostly independent of initial conditions. Further research into this model includes studying alternative STPBD games such as the Hawk-Dove game, using different grid structures, applying noise to the game, and changing the independent variables in the payoff matrix. We aim to give a more general approach to scoring these games that will map a cell and its neighborhood deterministically and directly onto a “cumulative” score, without concerning ourselves with two person interactions. The advantages of this are in its simplicity of representation and computation as well as its flexibility in representing the payoffs of every STPBD game yet studied. It is also capable of representing payoffs that could not be represented as sums of two person interactions. This system avoids the pitfalls of “equivalency regions,” payoffs which are numerically different, but are identical in simulation because of their underlying ordering. Once we have defined our system, we will be equipped to classify the immediate behavior of several small configurations of cooperators and defectors located in an innite sea of the other. This will serve as a demonstration of the usefulness of generality in this system.